Room-based maps

There are a couple of different ways to go about creating room-based maps. We'll look at doing this by generating random rectangles, by using random BSP trees and Waveform Function Collapse (WFC).

Random Rectangles

The easiest way to create rooms, is to just generate some random rectangles.

Here is a basic example graph: 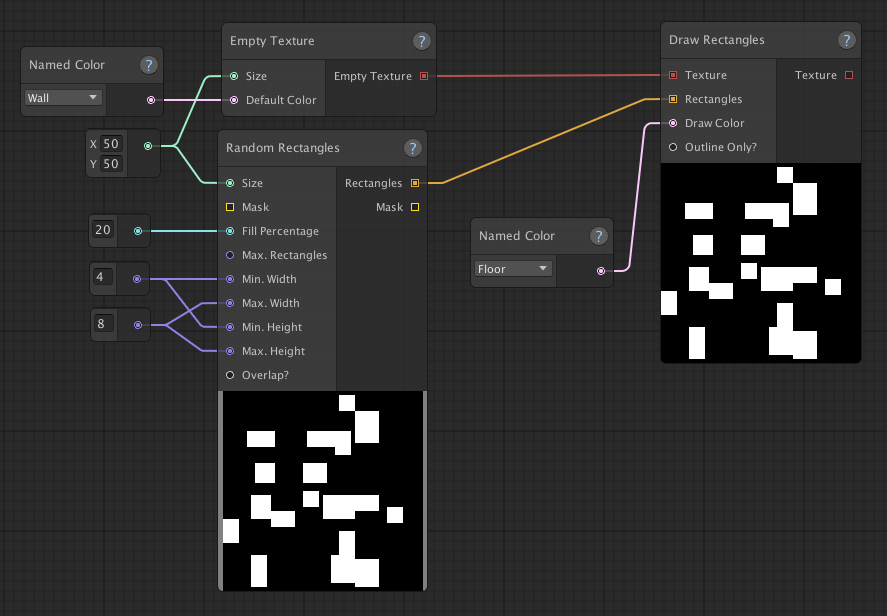This graph creates rooms by filling a 50x50 area for approximately 20% with random rectangles. The rectangles have a minimum size of 4x4 and a maximum size of 8x8. These rectangles are then drawn as floors on top of a texture that's filled with the color representing walls.

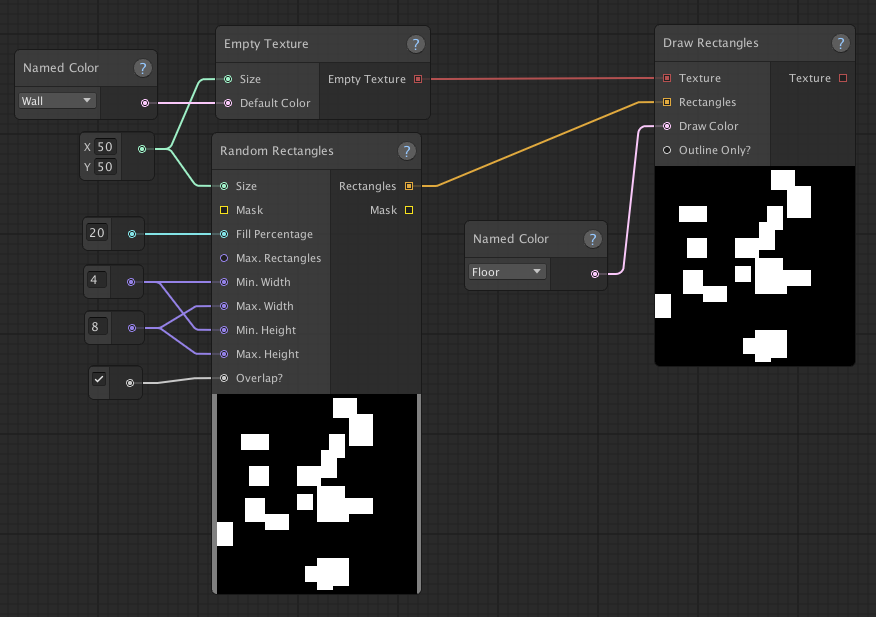
By default the randomly placed rectangles don't overlap. You can change this behaviour by setting "Overlap?" to true, like this:

BSP Trees

Another way to generate room-based maps, is to use Binary Space Partitioning (or BSP) trees. Simply put, a BSP tree divides an area (or space) into smaller spaces, by dividing a space into two spaces (hence the "binary" part) and splitting the resulting two spaces again, until the targeted number of divisions to make has been reached.

Here is a basic example 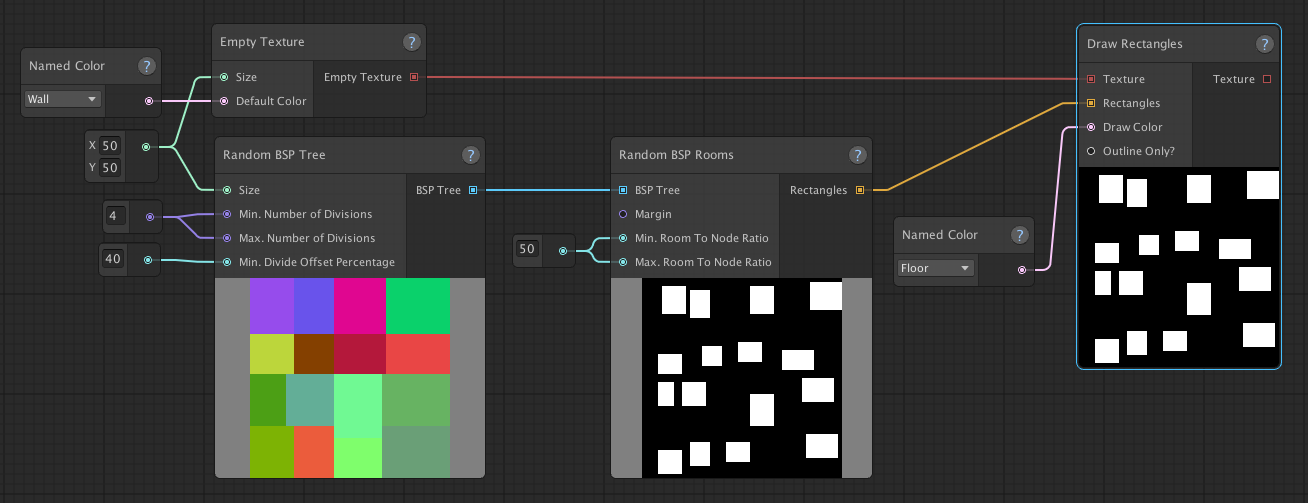graph: This graph creates rooms by first generating a BSP Tree, which divides a space of 50x50 into 16 smaller spaces. The Random BSP Rooms node then takes these spaces and generates a rectangle inside each of them, which are then drawn onto a texture in the same way as in the Random Rectangles example graph.

The advantage of this approach is that the resulting rooms will be guaranteed to be evenly distributed. The downside may be that it results in maps looking more alike than ones that you would create using a Random Rectangles node.

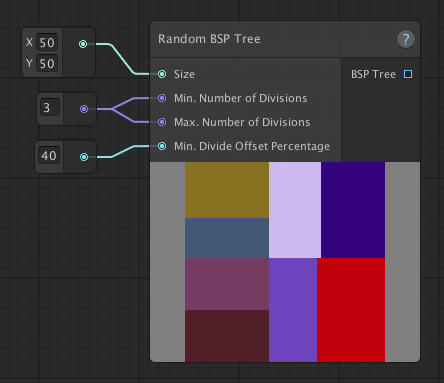
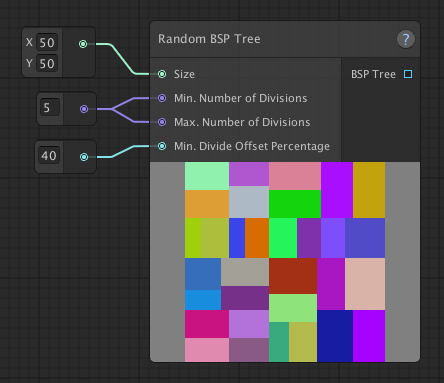
Number of divisions

The Random BSP Tree node will pick a number between Min. Number of Divisions and Max. Number of Divisions, the space will be divided that number of times. So in order to increase/decrease the number of spaces/rooms you want, you can increase/decrease these values.

The number of spaces you will end up will 2 by the power of the number of divisions. In the example above: 2^4 divisions = 16 spaces.

Less divisions (3)	More divisions (5)

If the Min. Number of Divisions and Max. Number of Divisions are set to the same value, it will result in the the same number of spaces/rooms each time the graph is run (though the divisions will be different). The greater the difference between these values, the more variety there will be in the number of spaces/rooms each time the graph is run.

Variety in space sizes

The Min. Divide Offset Percentage basically describes the maximum allowed size difference between two spaces, as the result of a division, can have with respect to each other. The value in the example, 40, means that neither space will take up less than 40% of the space they originate from.

Min. Divide Offset 25%	Min. Divide Offset 50%
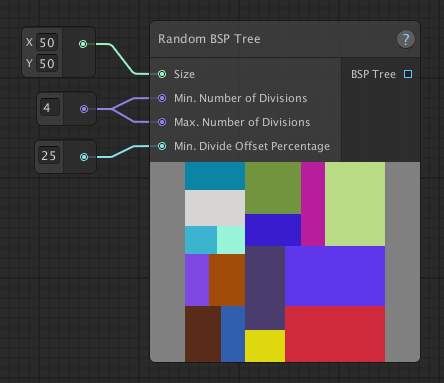Each time a space is split, neither of resulting spaces should be smaller than 25% of that original space.	Each time a space is split, neither of the resulting spaces should be smaller than 50%. This results in spaces being split evenly each time a division is made.

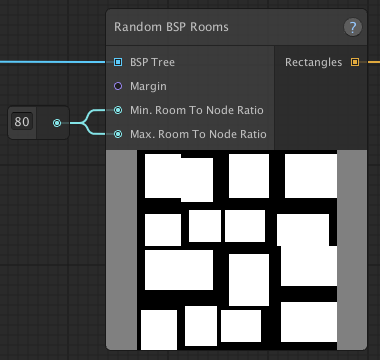
Room sizes

The Random BSP Rooms node generates random rectangles for each space inside of the BSP tree. By adjusting the values for Min. Room To Node Ratio and Max. Room To Node Ratio, the generated rooms will be either smaller or larger. The room to node ratio is a percentage that describes what amount of its space the generated rectangle should cover.

Smaller Room to Node Ratio (20)	Bigger Room to Node Ratio (80)

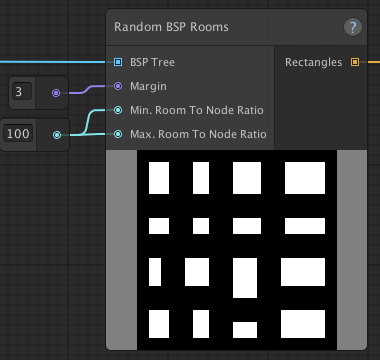
Room margins

As you may notice, some of the rooms are touching, merging together. This might not be what you want and you can avoid this by setting a Margin value.

Margin of 1	Margin of 3

Waveform Function Collapse (WFC)

WFC is an algorithm that's able to generate all kinds of random patterns based on a provided sample texture. To learn more about the WFC node, please check out the node index.

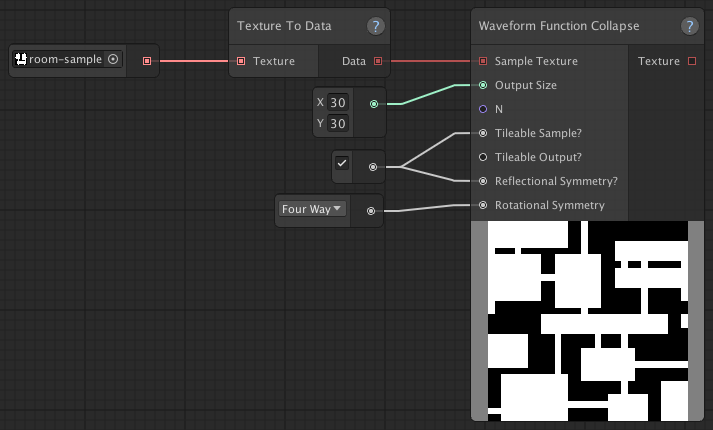
Here is the sample used (room-sample):

Connecting rooms

We've already seen how to connect different areas in this section of the "Adding more nodes" tutorial.

However, the Draw Connections (Shortest Path) node used there, is probably not what you want to use here. Instead, you can use the Draw Connections (Manhattan) variant, to draw connections by only using horizontal and vertical lines, like this: